Backpropagation

Gradient Descent Solution

def gradient_descent_update(x, gradx, learning_rate):
    """
    Performs a gradient descent update.
    """
    x = x - learning_rate * gradx
    # Return the new value for x
    return x

We adjust the old x pushing it in the opposite direction of gradx with the force learning_rate. Subtracting learning_rate * gradx. Remember the gradient is initially in the direction of steepest ascent so subtracting learning_rate * gradx from x turns it into steepest descent. You can make sure of this yourself by replacing the subtraction with an addition.

The Gradient & Backpropagation

Now that we know how to update our weights and biases using the gradient, we need to figure out how to calculate the gradients for all of our nodes. For each node, we'll want to change the values based on the gradient of the cost with respect to the value of that node. In this way, the gradient descent updates we make will eventually converge to the minimum of the cost.

Let's consider a network with a linear node l_1, a sigmoid node s, and another linear node l_2, followed by an MSE node to calculate the cost, C.

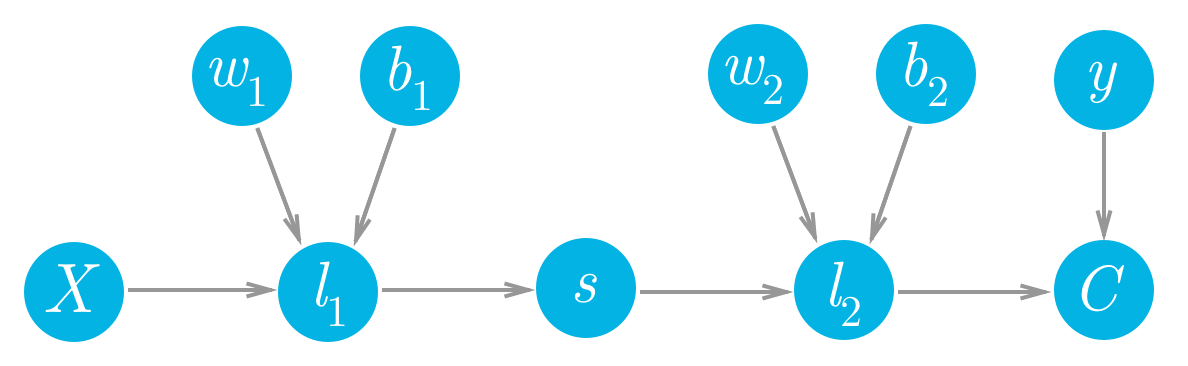
Forward pass for a simple two layer network.

Writing this out in MiniFlow, it would look like:

X, y = Input(), Input()
W1, b1 = Input(), Input()
W2, b2 = Input(), Input()

l1 = Linear(X, W1, b1)
s = Sigmoid(l1)
l2 = Linear(s, W2, b2)
cost = MSE(l2, y)

We can see that each of the values of these nodes flows forwards and eventually produces the cost C. For example, the value of the second linear node l_2 goes into the cost node and determines the value of that node. Accordingly, a change in l_2 will produce a change in C. We can write this relationship between the changes as a gradient,

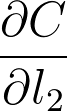
This is what a gradient means, it's a slope, how much you change the cost \partial C given a change in l_2, \partial l_2. So a node with a larger gradient with respect to the cost is going to contribute a larger change to the cost. In this way, we can assign blame for the cost to each node. The larger the gradient for a node, the more blame it gets for the final cost. And the more blame a node has, the more we'll update it in the gradient descent step.

If we want to update one of the weights with gradient descent, we'll need the gradient of the cost with respect to those weights. Let's see how we can use this framework to find the gradient for the weights in the second layer, w_2. We want to calculate the gradient of C with respect to w_2:

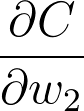
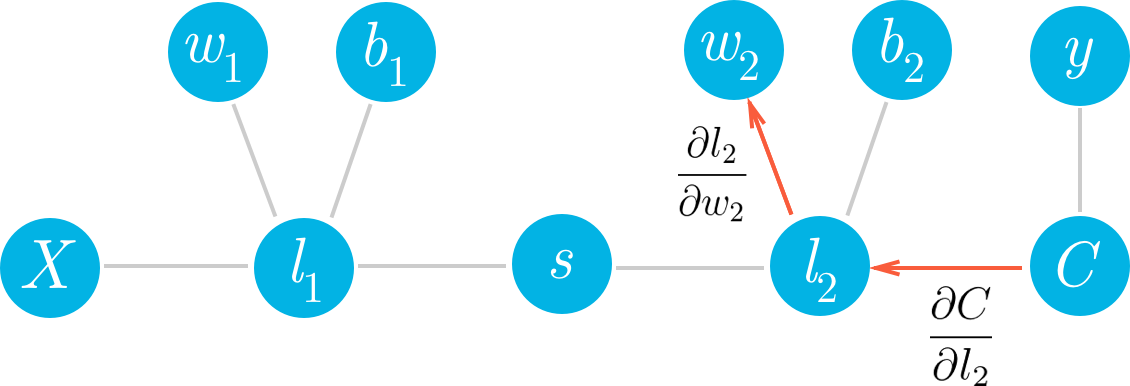
We can see in the graph that w_2 is connected to l_2, so a change in w_2 is going to create a change in l_2 which then creates a change in C. We can assign blame to w_2 by sending the cost gradient back through the network. First you have how much l_2 affected C, then how much w_2 affected l_2. Multiplying these gradients together gets you the total blame attributed to w_2.

Pre-requisites

Below we're getting into the math behind backpropagation which requires multivariable calculus. If you need a refresher, I highly recommend checking out

Khan Academy's lessons on partial derivatives
Another video on gradients
And finally, using the chain rule

Continuing on

Multiplying these gradients is just an application of the chain rule:

You can see in the graph w_2, l_2, and C are chained together. Any change in w_2 will create a change in l_2 and the size of that change is given by the gradient \partial l_2 / \partial w_2. Now, since l_2 is changing this will cause a change in the cost C and the size of that change is given by the gradient \partial C / \partial l_2. You can think of the chain rule similarly to the domino effect, changing something in the network will propagate through it altering other nodes along the way.

If you think of the chain rule as normal fractions, you can see that \partial l_2 in the denominator and numerator cancel out and you get back \partial C / \partial w_2 (although it doesn't exactly work like normal fractions, but it helps to keep track of things.) Okay, let's work out the gradient for w_2. First, we need to know the gradient for l_2.

As a reminder the cost is

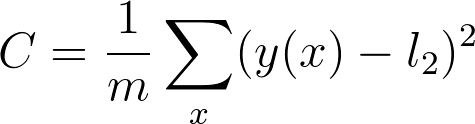
And the value for the second linear node is

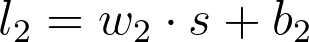
where w_2, s , and b_2 are all vectors and w_2 \cdot s means the dot product of w_2 and s .

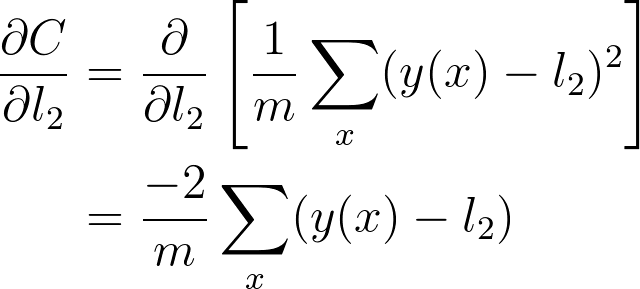
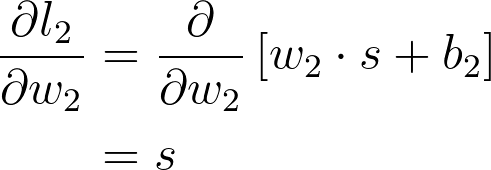
And putting these together, you get the gradient for w_2

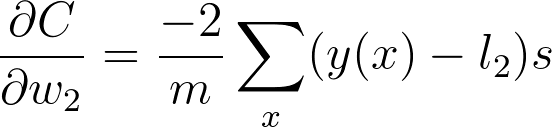
This is the gradient you use in the gradient descent update for w_2. You can see what we did here, we walked back through the graph and multiplied all the gradients we found along the way.

Now, let's go deeper and calculate the gradient for w_1. Here we use the same method as before, walking backwards through the graph.

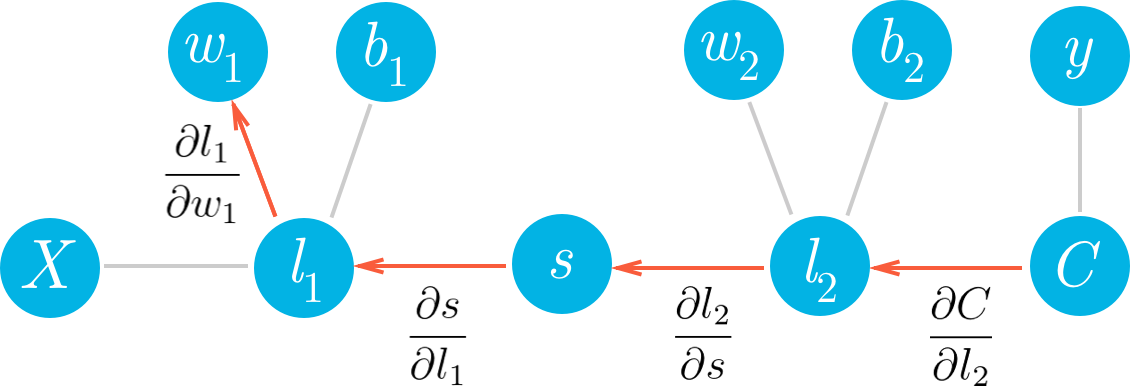
Hopefully it's clear now how to write out the gradient for w_1 just by looking at the graph. Using the chain rule, we'll write out the gradients for each node going backwards through the graph until we get to w_1.

Now we can start calculating each gradient in this expression to get the gradient for w_1

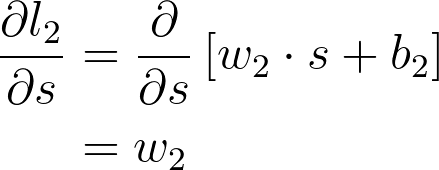
The next part is the gradient of the sigmoid function, s = f(l_1). Since we're using the logistic function here, the derivative can be written in terms of the sigmoid itself

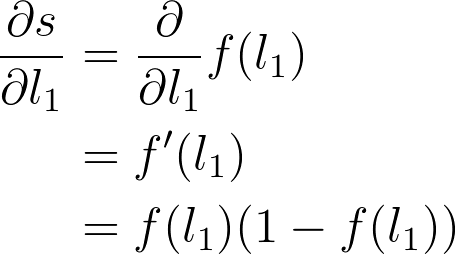
Putting this all together, you get

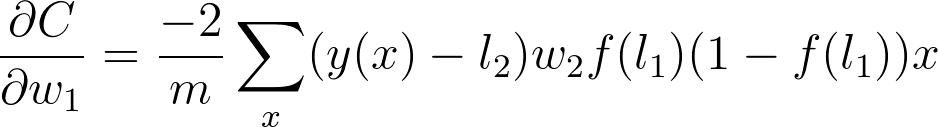
Now we can see a clear pattern. To find the gradient, you just multiply the gradients for all nodes in front of it going backwards from the cost. This is the idea behind backpropagation. The gradients are passed backwards through the network and used with gradient descent to update the weights and biases. If a node has multiple outgoing nodes, you just sum up the gradients from each node.

Implementing in MiniFlow

Let's think about how to translate this into MiniFlow. Looking at the graph, you see that each node gets the cost gradient from it's outbound nodes. For example, the node l_1 gets \partial C / \partial l_1 through the sigmoid node, s. Then l_1 passes on the cost gradient to the weight node w_1, but multiplied by \partial l_1 / \partial w_1, the gradient of l_1 with respect to it's input w_1.

So, each node will pass on the cost gradient to its inbound nodes and each node will get the cost gradient from it's outbound nodes. Then, for each node we'll need to calculate a gradient that's the cost gradient times the gradient of that node with respect to its inputs. Below I've written out this process for a Linear node.

# Initialize a partial for each of the inbound_nodes.
self.gradients = {n: np.zeros_like(n.value) for n in self.inbound_nodes}
# Cycle through the outputs. The gradient will change depending
# on each output, so the gradients are summed over all outputs.
for n in self.outbound_nodes:
    # Get the partial of the cost with respect to this node.
    grad_cost = n.gradients[self]
    # Set the partial of the loss with respect to this node's inputs.
    self.gradients[self.inbound_nodes[0]] += np.dot(grad_cost, self.inbound_nodes[1].value.T)
    # Set the partial of the loss with respect to this node's weights.
    self.gradients[self.inbound_nodes[1]] += np.dot(self.inbound_nodes[0].value.T, grad_cost)
    # Set the partial of the loss with respect to this node's bias.
    self.gradients[self.inbound_nodes[2]] += np.sum(grad_cost, axis=0, keepdims=False)

New Code

There have been a couple of changes to MiniFlow since we last took it for a spin:

The first being the Node class now has a backward method, as well as a new attribute self.gradients, which is used to store and cache gradients during the backward pass.

class Node(object):
    """
    Base class for nodes in the network.

    Arguments:

        `inbound_nodes`: A list of nodes with edges into this node.
    """
    def __init__(self, inbound_nodes=[]):
        """
        Node's constructor (runs when the object is instantiated). Sets
        properties that all nodes need.
        """
        # A list of nodes with edges into this node.
        self.inbound_nodes = inbound_nodes
        # The eventual value of this node. Set by running
        # the forward() method.
        self.value = None
        # A list of nodes that this node outputs to.
        self.outbound_nodes = []
        # New property! Keys are the inputs to this node and
        # their values are the partials of this node with
        # respect to that input.
        self.gradients = {}
        # Sets this node as an outbound node for all of
        # this node's inputs.
        for node in inbound_nodes:
            node.outbound_nodes.append(self)

    def forward(self):
        """
        Every node that uses this class as a base class will
        need to define its own `forward` method.
        """
        raise NotImplementedError

    def backward(self):
        """
        Every node that uses this class as a base class will
        need to define its own `backward` method.
        """
        raise NotImplementedError

The second change is to the helper function forward_pass(). That function has been replaced with forward_and_backward().

def forward_and_backward(graph):
    """
    Performs a forward pass and a backward pass through a list of sorted nodes.

    Arguments:

        `graph`: The result of calling `topological_sort`.
    """
    # Forward pass
    for n in graph:
        n.forward()

    # Backward pass
    # see: https://docs.python.org/2.3/whatsnew/section-slices.html
    for n in graph[::-1]:
        n.backward()

Setup

Here's the derivative of the sigmoid function w.r.t x:

sigmoid(x) = 1 / (1 + exp(-x))

\frac {\partial sigmoid}{\partial x} = sigmoid(x) * (1 - sigmoid(x))

Complete the implementation of backpropagation for the Sigmoid node by finishing the backward method in miniflow.py.
The backward methods for all other nodes have already been implemented. Taking a look at them might be helpful.

Question:

Start Quiz:

nn.py miniflow.py

"""
Test your network here!

No need to change this code, but feel free to tweak it
to test your network!

Make your changes to backward method of the Sigmoid class in miniflow.py
"""

import numpy as np
from miniflow import *

X, W, b = Input(), Input(), Input()
y = Input()
f = Linear(X, W, b)
a = Sigmoid(f)
cost = MSE(y, a)

X_ = np.array([[-1., -2.], [-1, -2]])
W_ = np.array([[2.], [3.]])
b_ = np.array([-3.])
y_ = np.array([1, 2])

feed_dict = {
    X: X_,
    y: y_,
    W: W_,
    b: b_,
}

graph = topological_sort(feed_dict)
forward_and_backward(graph)
# return the gradients for each Input
gradients = [t.gradients[t] for t in [X, y, W, b]]

"""
Expected output

[array([[ -3.34017280e-05,  -5.01025919e-05],
       [ -6.68040138e-05,  -1.00206021e-04]]), array([[ 0.9999833],
       [ 1.9999833]]), array([[  5.01028709e-05],
       [  1.00205742e-04]]), array([ -5.01028709e-05])]
"""
print(gradients)

"""
Implement the backward method of the Sigmoid node.
"""
import numpy as np


class Node(object):
    """
    Base class for nodes in the network.

    Arguments:

        `inbound_nodes`: A list of nodes with edges into this node.
    """
    def __init__(self, inbound_nodes=[]):
        """
        Node's constructor (runs when the object is instantiated). Sets
        properties that all nodes need.
        """
        # A list of nodes with edges into this node.
        self.inbound_nodes = inbound_nodes
        # The eventual value of this node. Set by running
        # the forward() method.
        self.value = None
        # A list of nodes that this node outputs to.
        self.outbound_nodes = []
        # New property! Keys are the inputs to this node and
        # their values are the partials of this node with
        # respect to that input.
        self.gradients = {}
        # Sets this node as an outbound node for all of
        # this node's inputs.
        for node in inbound_nodes:
            node.outbound_nodes.append(self)

    def forward(self):
        """
        Every node that uses this class as a base class will
        need to define its own `forward` method.
        """
        raise NotImplementedError

    def backward(self):
        """
        Every node that uses this class as a base class will
        need to define its own `backward` method.
        """
        raise NotImplementedError


class Input(Node):
    """
    A generic input into the network.
    """
    def __init__(self):
        # The base class constructor has to run to set all
        # the properties here.
        #
        # The most important property on an Input is value.
        # self.value is set during `topological_sort` later.
        Node.__init__(self)

    def forward(self):
        # Do nothing because nothing is calculated.
        pass

    def backward(self):
        # An Input node has no inputs so the gradient (derivative)
        # is zero.
        # The key, `self`, is reference to this object.
        self.gradients = {self: 0}
        # Weights and bias may be inputs, so you need to sum
        # the gradient from output gradients.
        for n in self.outbound_nodes:
            grad_cost = n.gradients[self]
            self.gradients[self] += grad_cost * 1


class Linear(Node):
    """
    Represents a node that performs a linear transform.
    """
    def __init__(self, X, W, b):
        # The base class (Node) constructor. Weights and bias
        # are treated like inbound nodes.
        Node.__init__(self, [X, W, b])

    def forward(self):
        """
        Performs the math behind a linear transform.
        """
        X = self.inbound_nodes[0].value
        W = self.inbound_nodes[1].value
        b = self.inbound_nodes[2].value
        self.value = np.dot(X, W) + b

    def backward(self):
        """
        Calculates the gradient based on the output values.
        """
        # Initialize a partial for each of the inbound_nodes.
        self.gradients = {n: np.zeros_like(n.value) for n in self.inbound_nodes}
        # Cycle through the outputs. The gradient will change depending
        # on each output, so the gradients are summed over all outputs.
        for n in self.outbound_nodes:
            # Get the partial of the cost with respect to this node.
            grad_cost = n.gradients[self]
            # Set the partial of the loss with respect to this node's inputs.
            self.gradients[self.inbound_nodes[0]] += np.dot(grad_cost, self.inbound_nodes[1].value.T)
            # Set the partial of the loss with respect to this node's weights.
            self.gradients[self.inbound_nodes[1]] += np.dot(self.inbound_nodes[0].value.T, grad_cost)
            # Set the partial of the loss with respect to this node's bias.
            self.gradients[self.inbound_nodes[2]] += np.sum(grad_cost, axis=0, keepdims=False)


class Sigmoid(Node):
    """
    Represents a node that performs the sigmoid activation function.
    """
    def __init__(self, node):
        # The base class constructor.
        Node.__init__(self, [node])

    def _sigmoid(self, x):
        """
        This method is separate from `forward` because it
        will be used with `backward` as well.

        `x`: A numpy array-like object.
        """
        return 1. / (1. + np.exp(-x))

    def forward(self):
        """
        Perform the sigmoid function and set the value.
        """
        input_value = self.inbound_nodes[0].value
        self.value = self._sigmoid(input_value)

    def backward(self):
        """
        Calculates the gradient using the derivative of
        the sigmoid function.
        """
        # Initialize the gradients to 0.
        self.gradients = {n: np.zeros_like(n.value) for n in self.inbound_nodes}

        # Cycle through the outputs. The gradient will change depending
        # on each output, so the gradients are summed over all outputs.
        for n in self.outbound_nodes:
            # Get the partial of the cost with respect to this node.
            grad_cost = n.gradients[self]
            """
            TODO: Your code goes here!

            Set the gradients property to the gradients with respect to each input.

            NOTE: See the Linear node and MSE node for examples.
            """


class MSE(Node):
    def __init__(self, y, a):
        """
        The mean squared error cost function.
        Should be used as the last node for a network.
        """
        # Call the base class' constructor.
        Node.__init__(self, [y, a])

    def forward(self):
        """
        Calculates the mean squared error.
        """
        # NOTE: We reshape these to avoid possible matrix/vector broadcast
        # errors.
        #
        # For example, if we subtract an array of shape (3,) from an array of shape
        # (3,1) we get an array of shape(3,3) as the result when we want
        # an array of shape (3,1) instead.
        #
        # Making both arrays (3,1) insures the result is (3,1) and does
        # an elementwise subtraction as expected.
        y = self.inbound_nodes[0].value.reshape(-1, 1)
        a = self.inbound_nodes[1].value.reshape(-1, 1)

        self.m = self.inbound_nodes[0].value.shape[0]
        # Save the computed output for backward.
        self.diff = y - a
        self.value = np.mean(self.diff**2)

    def backward(self):
        """
        Calculates the gradient of the cost.

        This is the final node of the network so outbound nodes
        are not a concern.
        """
        self.gradients[self.inbound_nodes[0]] = (2 / self.m) * self.diff
        self.gradients[self.inbound_nodes[1]] = (-2 / self.m) * self.diff


def topological_sort(feed_dict):
    """
    Sort the nodes in topological order using Kahn's Algorithm.

    `feed_dict`: A dictionary where the key is a `Input` Node and the value is the respective value feed to that Node.

    Returns a list of sorted nodes.
    """

    input_nodes = [n for n in feed_dict.keys()]

    G = {}
    nodes = [n for n in input_nodes]
    while len(nodes) > 0:
        n = nodes.pop(0)
        if n not in G:
            G[n] = {'in': set(), 'out': set()}
        for m in n.outbound_nodes:
            if m not in G:
                G[m] = {'in': set(), 'out': set()}
            G[n]['out'].add(m)
            G[m]['in'].add(n)
            nodes.append(m)

    L = []
    S = set(input_nodes)
    while len(S) > 0:
        n = S.pop()

        if isinstance(n, Input):
            n.value = feed_dict[n]

        L.append(n)
        for m in n.outbound_nodes:
            G[n]['out'].remove(m)
            G[m]['in'].remove(n)
            # if no other incoming edges add to S
            if len(G[m]['in']) == 0:
                S.add(m)
    return L


def forward_and_backward(graph):
    """
    Performs a forward pass and a backward pass through a list of sorted Nodes.

    Arguments:

        `graph`: The result of calling `topological_sort`.
    """
    # Forward pass
    for n in graph:
        n.forward()

    # Backward pass
    # see: https://docs.python.org/2.3/whatsnew/section-slices.html
    for n in graph[::-1]:
        n.backward()

Solution:

Next Concept